LES CALCULS AVEC LES RÉSISTANCES

 

Et oui, vous n'y échapperais pas, en électronique, y'a aussi des maths ! :-(

Mais bon, ces calculs sont à la portée de tous, même des mathophobes !

En électronique, quand on fait des maths, il ne faut pas perdre de vue que les résultats que nous trouvons doivent être coérrants, en effet, si vous faites un montage avec une pile 9 volts et que vous calculez un courant de 10A, il y a un problème ! (10A à fournir par la pile...elle risque de vite s'épuiser la pauvre ! ). Pensez à ce que vous faites et ne foncez pas tête baissée dans les maths sans penser au système réel !

 

Bon ! ceci étant dit, pour les calculs avec les résistances, c'est assez simple !

 

ATTENTION AUX CONVENTIONS !!! LA RÉSISTANCE EST UN RÉCEPTEUR, DONC LE COURANT ENTRE DANS LA RÉSISTANCE ET LA TENSION EST FLÈCHE DANS L'AUTRE SENS !!!!!!!!!

 

 

 

Commençons par la loi Fondamentale : La LOI D'OHMS !

On a ceci :

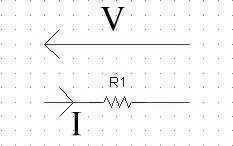
La loi d'Ohms est une loi qui permet d'exprimer la tension en fonction du courant et de la résistance, qui est :

U = R * I

Cette relation est TRÈS IMPORTANTE, gravez la dans votre esprit car vous vous en servirez très souvent !

 

Voyons Les calculs de résistances équivalentes.

 

RÉSISTANCES SÉRIES

Imaginons que vous ayez 3 résistances en série, en série veux dire traversées par le même courant :

Et on veux connaître la résistance équivalente vue entre A et B, Quelle est donc sa valeur ??

très simple : R équivalent = R1 + R2 + R3.

Et oui, c'est tout simplement la somme des 3 résistances...

 

 

RÉSISTANCES PARALLÈLES

Reprenons nos 3 résistances, cette fois câblées ainsi :

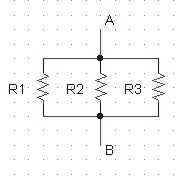
On dit qu'elles sont en parallèles, c'est à dire qu'elles ont la même tension à leur bornes

On veux encore connaître la résistance équivalente entre A et B, Quelle est cette valeur ?

La, il faut faire appel à une autre notion, l'admittance des résistances. L'admittance de la résistance est tout simplement l'inverse de cette résistance

Souvent notée Y, on dit que Y = 1/R.

On a donc : Y équivalent = Y1 + Y2 + Y3

Ou bien : 1/R = 1/R1 + 1/R2 + 1/R3

 

 

Résumé à retenir :

Pour des résistances en série : La résistance équivalente = somme des résistances

Pour des résistances en parrallèles : Inverse de la résistance équivalente = Somme des inverses des Résistances

 

 

Bien sur, pour vous embêter un peu, vous trouverai sûrement des problèmes avec des résistances en séries et en parallèles comme ça :

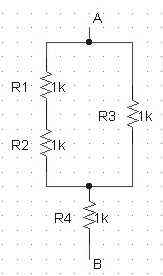
Et bien, il suffit de regarder le schéma et voir quelles résistances sont parcourus par le même courant :

Ici R1 et R2 parcourues par le même courant donc R1 et R2 en série.

On posera R1+R2=R'

Ensuite la résistance R' et R3 ont la même tension à leurs bornes donc :

R3 parralèle à R' => R3//R' = R''

Bon très bien, on vois enfin que R'' et R4 sont traversées par le même courant, donc R4 et R'' sont en série :

Rab = R'' + R4

petite astuce : quand 2 résistances sont en parallèle, la résistance équivalente c'est le produit des résistances divisée par la somme, dans notre exemple :

R''=(R'*R3)/(R3+R')

 

Donc en résumé on a R''=(R'*R3) / (R'+R3) c'est a dire R''=[ (R1+R2)*R3 ] / [ R1 + R2 +R3 ]

 

Rab = R'' + R4 = R4 + [ (R1+R2)*R3 ] / [ R1 + R2 +R3 ]

 

Un petit conseil : exercez vous sur des montages comme cela, au bon du 10eme vous serez INCOLLABLE !

 

PUISSANCE DANS UNE RÉSISTANCE

 

Il est parfois très utile, pour choisir sa résistance de pouvoir calculer la puissance dissipée par celle ci :

On a ce schéma :

 

Alors P=R*I²=U²/R